Improving Diffusion Inverse Problem Solving with Decoupled Noise Annealing

Bingliang Zhang*,1, Wenda Chu*,1, Julius Berner1,2, Chenlin Meng3, Anima Anandkumar1, Yang Song3,
1California Institute of Technology    2NVIDIA    3Stanford University    4OpenAI
* Equal Contribution
CVPR 2025
Paper arXiv Code

Overview of Decoupled Annealing Posterior Sampling (DAPS). Our method provides a flexible and effective framework for solving inverse problems through a decoupled posterior sampling process. In (a)(b), we present DAPS visual results on FFHQ and ImageNet at a resolution of 256, and in (c), on natural images at a resolution of 768. In (d), we display DAPS results on compressed sensing multi-coil MRI (CS-MRI). DAPS effectively addresses nonlinear inverse problems as well as medical imaging MRI challenges. Additionally, DAPS can be enhanced using large-scale latent diffusion models, as shown in (c).

Abstract

Diffusion models have recently achieved success in solving Bayesian inverse problems with learned data priors. Current methods build on top of the diffusion sampling process, where each denoising step makes small modifications to samples from the previous step. However, this process struggles to correct errors from earlier sampling steps, leading to worse performance in complicated nonlinear inverse problems, such as phase retrieval. To address this challenge, we propose a new method called Decoupled Annealing Posterior Sampling (DAPS) that relies on a novel noise annealing process. Specifically, we decouple consecutive steps in a diffusion sampling trajectory, allowing them to vary considerably from one another while ensuring their time-marginals anneal to the true posterior as we reduce noise levels. This approach enables the exploration of a larger solution space, improving the success rate for accurate reconstructions. We demonstrate that DAPS significantly improves sample quality and stability across multiple image restoration tasks, particularly in complicated nonlinear inverse problems.

Method

We propose Decoupled Annealing Posterior Sampling (DAPS) algorithm, which incorporates a pre-trained diffusion model as a prior to solve general inverse problems. By iteratively sampling from the time-marginal distribution, our method creates approximate samples from the posterior distribution.


Demo of how DAPS works

        

Experimental Results

2D Synthetic Data

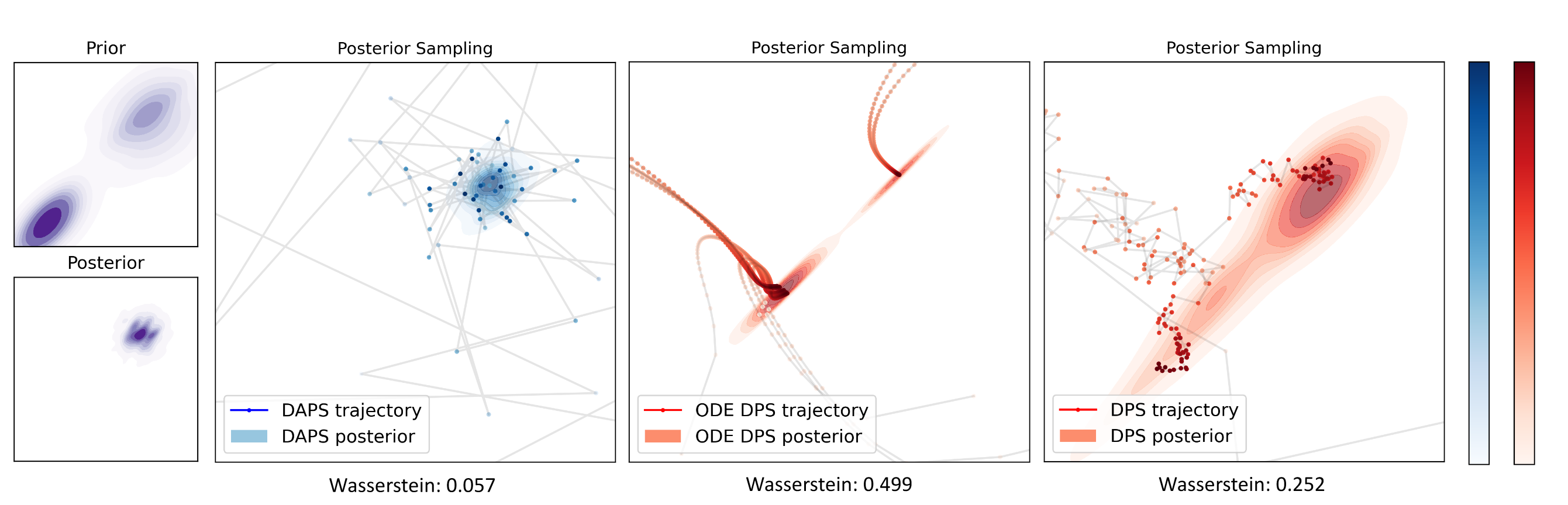
We compare DAPS with DPS on a nonlinear inverse problem with a 2D Gaussian mixture prior. DAPS is able to sample more accurately from the posterior distribution.


Image Restoration

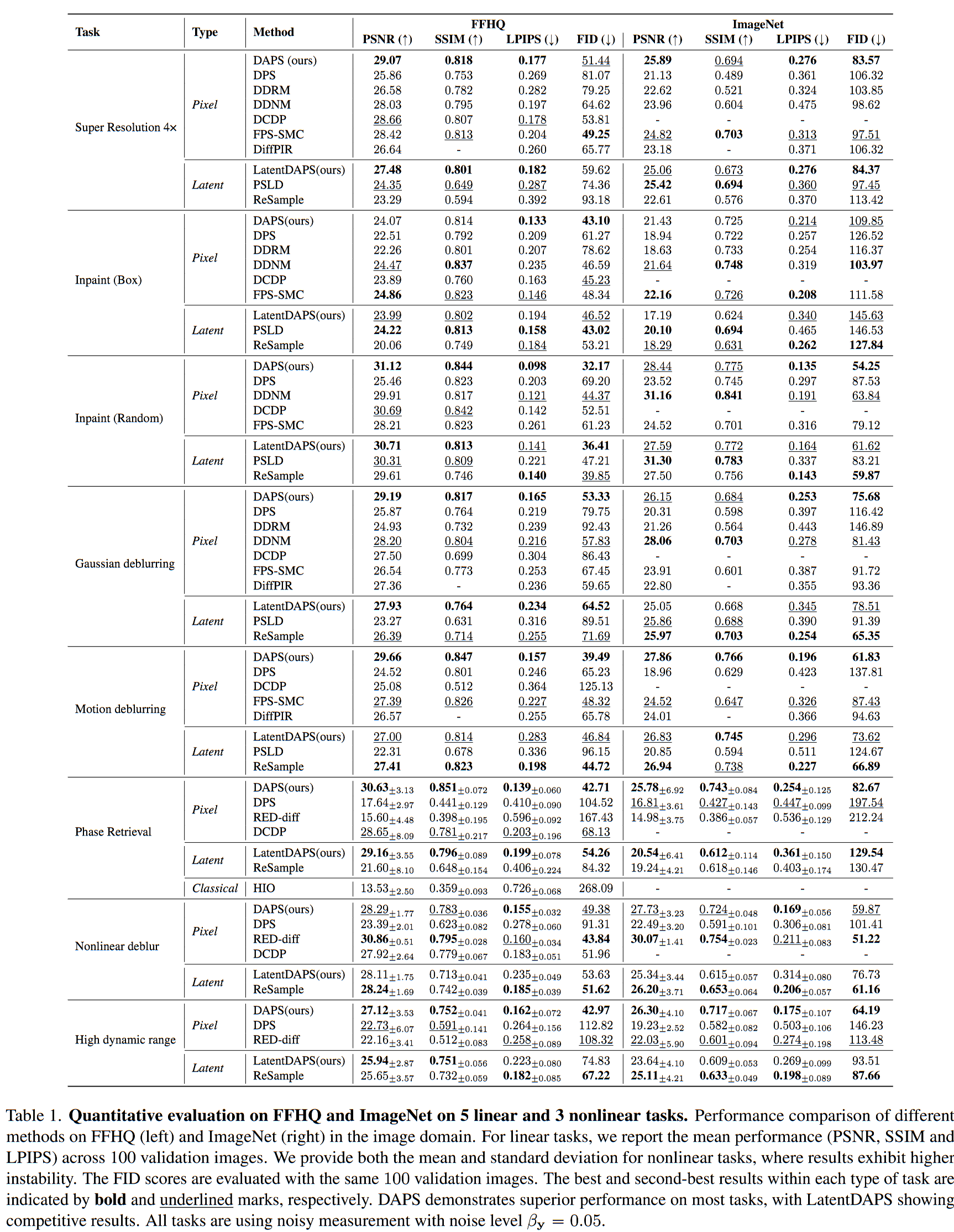
We evaluate DAPS with a series of inverse problems in image domain, including five linear inverse problems: (1) super-resolution, (2) Gaussian deblurring, (3) motion deblurring, (4) inpainting with a box mask, (5) inpainting on random pixels, and three nonlinear inverse problems: (1) phase retrieval, (2) nonlinear deblurring, (3) high dynamic range reconstruction. DAPS outperforms existing baselines in terms of perceptual quality (LPIPS) and peak signal-to-noise ratio (PSNR).

DAPS with Stable Diffusion

DAPS can also be applied to large-scale text-conditioned latent diffusion models, e.g., Stable Diffusion.

Sampling results of LatentDAPS (SD v1.5) on FFHQ 256x256 images. The images are sampled with a guidance scale of 7.5 and a text prompt "a natural looking human face."

Compressed Sensing MRI

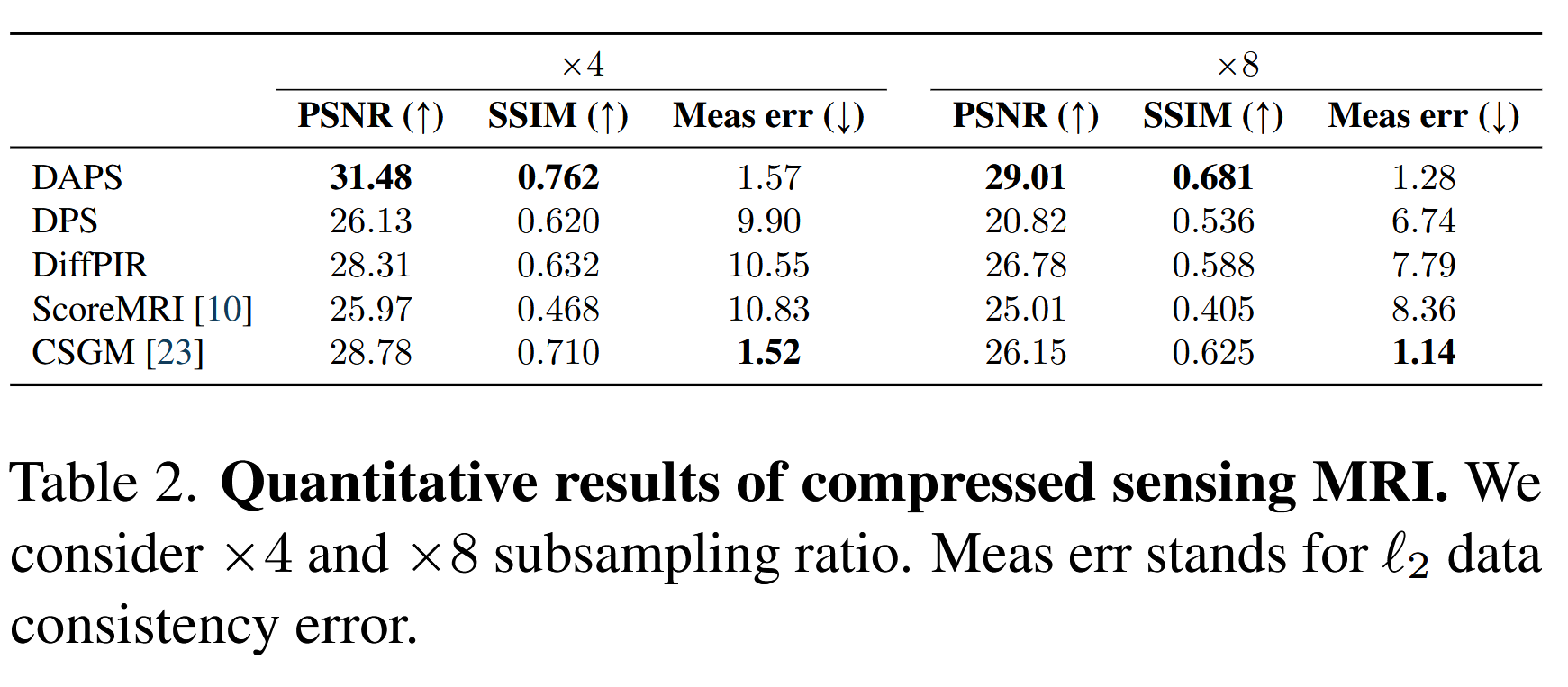
We apply DAPS to solve the compressed sensing multi-coil magnetic resonance imaging problem (CS-MRI).

Sample Diversity

DAPS is able to generate diverse samples given less information. For example, we show several generated samples for (1) inpainting with large boxes and (2) 16x super-resolution.

Time Efficiency

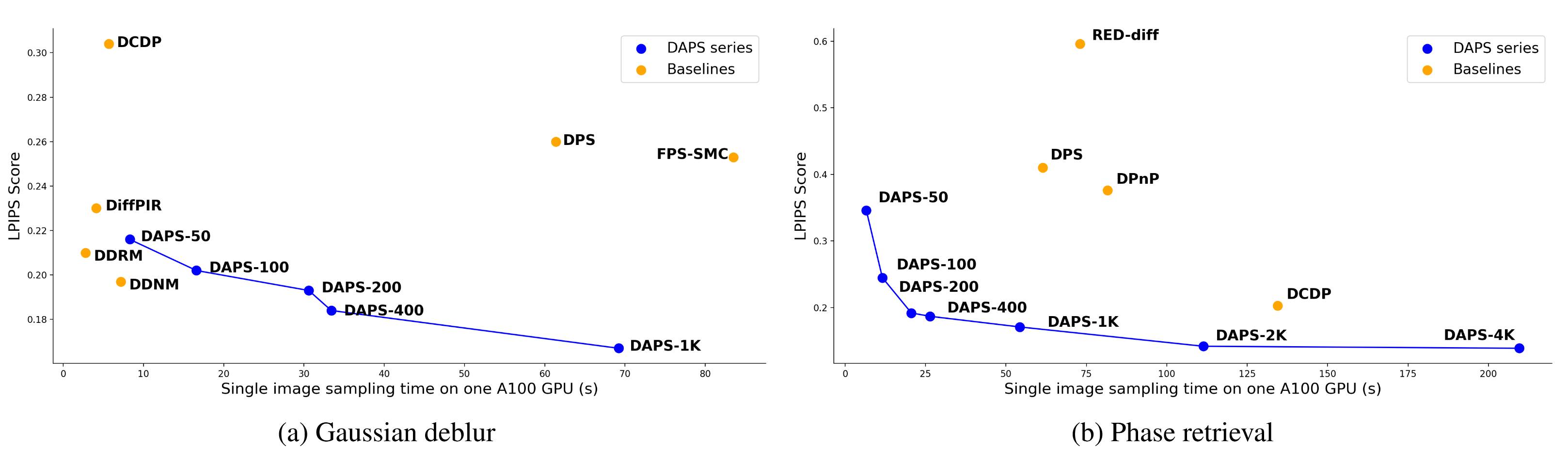
We run DAPS with various configurations to test its performance under different computing budgets in terms of the number of function evaluation (NFEs). DAPS is able to generate high-quality samples with a modest time cost.

Acknowledgements

We are grateful to Pika for providing the computing resources essential for this research. We also extend our thanks to the Kortschak Scholars Fellowship for supporting B.Z. and W.C. at Caltech. J.B. acknowledges support from the Wally Baer and Jeri Weiss Postdoctoral Fellowship. A.A. is supported in part by Bren endowed chair and by the AI2050 senior fellow program at Schmidt Sciences.

BibTeX

@misc{zhang2024improvingdiffusioninverseproblem,
      title={Improving Diffusion Inverse Problem Solving with Decoupled Noise Annealing}, 
      author={Bingliang Zhang and Wenda Chu and Julius Berner and Chenlin Meng and Anima Anandkumar and Yang Song},
      year={2024},
      eprint={2407.01521},
      archivePrefix={arXiv},
      primaryClass={cs.LG},
      url={https://arxiv.org/abs/2407.01521}, 
}